Proof of the formula for wave speed

We start with the simple formula for speed:

Speed = distance/time in other words speed is the distance travelled in one second.

The frequency (f) of w a wave is how any vibrations per second the wave makes at a particular point
The wavelength (l) of a wave is the distance between 'similar' points on the wave. That is, for example, crest-to-crest or trough-to- trough.

Now if f waves move past appoint in one second the distance travelled by the wave is f whole wavelengths. (See Figure 1 (a) and (b))




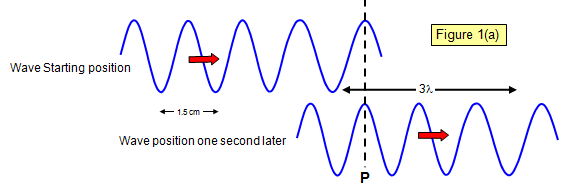
In Figure 1(a) the wavelength of the wave is 1.5 cm and three waves pass the point P every second. This means that the frequency of the wave is 3 Hz and the speed of the wave is 3x1.5 = 4.5 cm/s.

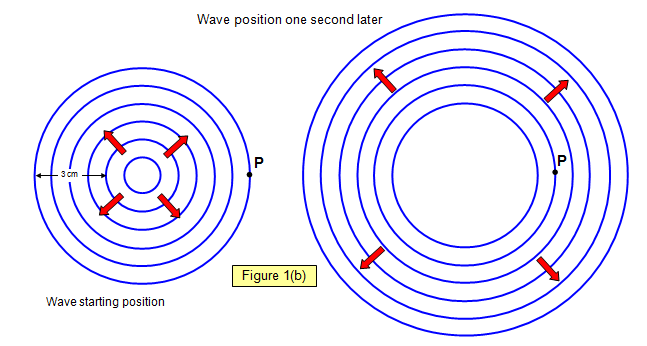
In Figure 1(b) the wavelength of the wave is 0.75 cm and four waves pass the point P every second. This means that the frequency of the wave is 4 Hz and the speed of the wave is 4x0.75 = 3 cm/s. But the distance travelled in one second is the speed and so: